2006　慶応義塾大学　理工学部MathJax

【１】

(1)　$a\text{，}b\text{，}c\text{，}d$は実数とする．関数

$f(x)=\{\begin{array}{ll}x-1& \text{（}x\leqq -1\text{）}\\ a{x}^2+bx+c& \text{（}-1<x<1\text{）}\\ d-2x& \text{（}1\leqq x\text{）}\end{array}$

がすべての$x$で微分可能であるとき，$a=\boxed{\text{(ア)}}\text{，}d=\boxed{\text{(イ)}}$である．

【１】

(2)　定積分

${\displaystyle {\int }_e^{e^e}}{\displaystyle \frac{\log (\log x)}{x\log x}}dx$

の値は$\boxed{\text{(ウ)}}$となる．

【１】

(3)　$\alpha \text{，}\beta$は実数とする．どのような実数$p\text{，}q$に対しても

${\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}}(p\cos x+q\sin x)(x^2+\alpha x+\beta )dx=0$

となるのは，$\alpha =\boxed{\text{(エ)}}\text{，}\beta =\boxed{\text{(オ)}}$のときである．

【２】　ある時点（$0$年目）で，同じ要領の$2$つの空の$\stackrel{\text{たる}}{\text{樽}}\text{，}\mathrm{A}\text{，}\mathrm{B}$に新$\stackrel{\text{みそ}}{\text{味噌}}$を一杯に入れ，以後，$1$年経つごとに以下の操作を行う．ただし味噌の量は自然には増減しないとする．

　$\mathrm{B}$の味噌を半分取り除き，$\mathrm{A}$の味噌の半分を$\mathrm{B}$に移す．さらに，$\mathrm{A}$にはその年の新味噌を入れ一杯にし，両樽ともよく混ぜる．

　以下では，新味噌は$0$年物とし，$x$年物の味噌が$1$年経過したものを$(x+1)$年物とする．また，$x$年物と$y$年物を同量ずつ混ぜた味噌は${\displaystyle \frac{x+y}{2}}$年物と呼ぶ．

　$n$年後に上記の操作を行った直後の$\mathrm{A}\text{，}\mathrm{B}$の味噌をそれぞれ$a_n$年物，$b_n$年物と表す．例えば$(a_1,b_1)=({\displaystyle \frac{1}{2}},1)\text{，}(a_2,b_2)=\boxed{\text{(カ)}}$となる．

　自然数$n$に対し，$a_{n+1}$を$a_n$で表すと$a_{n+1}=\boxed{\text{(キ)}}$となり，数列$\{a_n\}$の一般項は$a_n=\boxed{\text{(ク)}}$となる．この式を用いることで，数列$\{b_n\}$の漸化式$b_{n+1}=\boxed{\text{(ケ)}}$を得る．ここで$c_n=2^n(b_n-3)$とおき，数列$\{c_n\}$の一般項を求めることにより，数列$\{b_n\}$の一般項は$b_n=\boxed{\text{(コ)}}$となることがわかる．

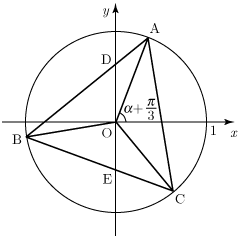
【３】　座標平面の原点$\mathrm{O}$を中心とする単位円周上に$3$点$\mathrm{A}(\cos (\alpha +{\displaystyle \frac{\pi }{3}}),\sin (\alpha +{\displaystyle \frac{\pi }{3}}\left)\right)\text{，}\mathrm{B}(\cos (\alpha +\pi ),\sin (\alpha +\pi ))\text{，}\mathrm{C}(\cos (\alpha +{\displaystyle \frac{5\pi }{3}}),\sin (\alpha +{\displaystyle \frac{5\pi }{3}}\left)\right)$をとる（右図参照）．ただし，$0\leqq \alpha <{\displaystyle \frac{\pi }{6}}$とする．以下，(サ)〜(ス)は$\cos \alpha \text{，}\sin \alpha$を用いて，(セ)〜(タ)は$\cos \alpha$を用いて記述しなさい．

　線分$\mathrm{AB}$と$y$軸との交点を$\mathrm{D}\text{，}$線分$\mathrm{BC}$と$y$軸との交点を$\mathrm{E}$とすると，線分$\mathrm{OD}\text{，}$線分$\mathrm{OE}$の長さはそれぞれ$\mathrm{OD}={\displaystyle \frac{1}{\boxed{\text{(サ)}}}}\text{，}\mathrm{OE}={\displaystyle \frac{1}{\boxed{\text{(シ)}}}}$である．

　この$xy$平面を含む座標空間において，正三角形$\mathrm{ABC}$内の各点から，$xy$平面と垂直に，高さがその点の$x$座標の絶対値である線分を立てて得られる立体図形を考える．頂点$\mathrm{A}\text{，}\mathrm{B}\text{，}\mathrm{C}$の上にある線分の最上点をそれぞれ$\mathrm{F}\text{，}\mathrm{G}\text{，}\mathrm{H}$とすると，三角錐$\mathrm{OADF}$の体積は${\displaystyle \frac{\mathrm{OD}}{24}}\times {(\boxed{\text{(ス)}})}^2\text{，}$四角錐$\mathrm{OACHF}$の体積は$\boxed{\text{(セ)}}$となる．

　$\mathrm{A}\text{，}\mathrm{C}\text{，}\mathrm{D}\text{，}\mathrm{E}\text{，}\mathrm{F}\text{，}\mathrm{H}$を頂点にもつ五面体の体積は，これら$2$つの錐体および三角錐$\mathrm{OCEH}$の体積の和であり，$\boxed{\text{(ソ)}}$となる．また，三角錐$\mathrm{BDEG}$の体積は$\boxed{\text{(タ)}}$となる．

【４】(1)　積分

$\theta ={\displaystyle {\int }_0^{1-r}}{\displaystyle \frac{dt}{\sqrt{1-t^2}}}\text{（}0<r<1\text{）}$

において，$1-r=\sin \alpha (0<\alpha <{\displaystyle \frac{\pi }{2}})$とおくと，$\theta =\alpha$であることを示しなさい．

(2)　関数

$r=1-\sin \theta (0<\theta <{\displaystyle \frac{\pi }{2}})$

を極方程式とする座標平面上（$x\text{，}y$座標）の曲線を考える．偏角$\theta$をもつ点における接線の傾き$u(\theta )={\displaystyle \frac{dy}{dx}}$は，$\theta$を用いて表すと$u(\theta )=\boxed{\text{(チ)}}$となり，

$\underset{\theta \to +0}{\lim }u(\theta )=\boxed{\text{(ツ)}}\text{，}\underset{\theta \to \frac{\pi }{2}-0}{\lim }u(\theta )=\boxed{\text{(テ)}}$

である．

(3)　(2)の曲線において，$y$座標が最大となる点を求め，曲線の概形を図示しなさい．解答は計算も含めて解答欄に書きなさい．

【５】　整数$p\text{，}q\text{，}r\text{，}\alpha \text{，}\beta$に対し，次のような$x\text{，}y$についての連立$1$次方程式を考える．

$\{\begin{array}{l}x+py=\alpha \\ qx+ry=\beta \end{array}$

以下では，$r-pq\ne 0$とする．

(1)　解$x\text{，}y$を$p\text{，}q\text{，}r\text{，}\alpha \text{，}\beta$を用いて表しなさい．解答欄には答だけを書きなさい．

(2)　整数$p\text{，}q\text{，}r$に関する条件$|r-pq|=1$は，任意の整数$\alpha \text{，}\beta$に対し解$x\text{，}y$が整数であるための必要十分条件であることを証明しなさい．

(3)　$|r-pq|=1$のとき，$(\alpha ,\beta )=(1,2)$に対する解の$x$の値が$2$となるような整数の組$(p,q,r)$をすべて求めなさい．