【2】 原点fを中心とする半径の円をとする.円に外接しながら,半径の円がすべることなく回転する.円の中心をとし,円上の点は最初,軸上の点にあるものとする.半直線上で点からの距離がの点をとし,が軸の正の向きとなす角をとする.が回転してがからまで変化するとき,点が描く曲線をとする.曲線の概形を図1に示す.以下の問いに答えよ.
 |
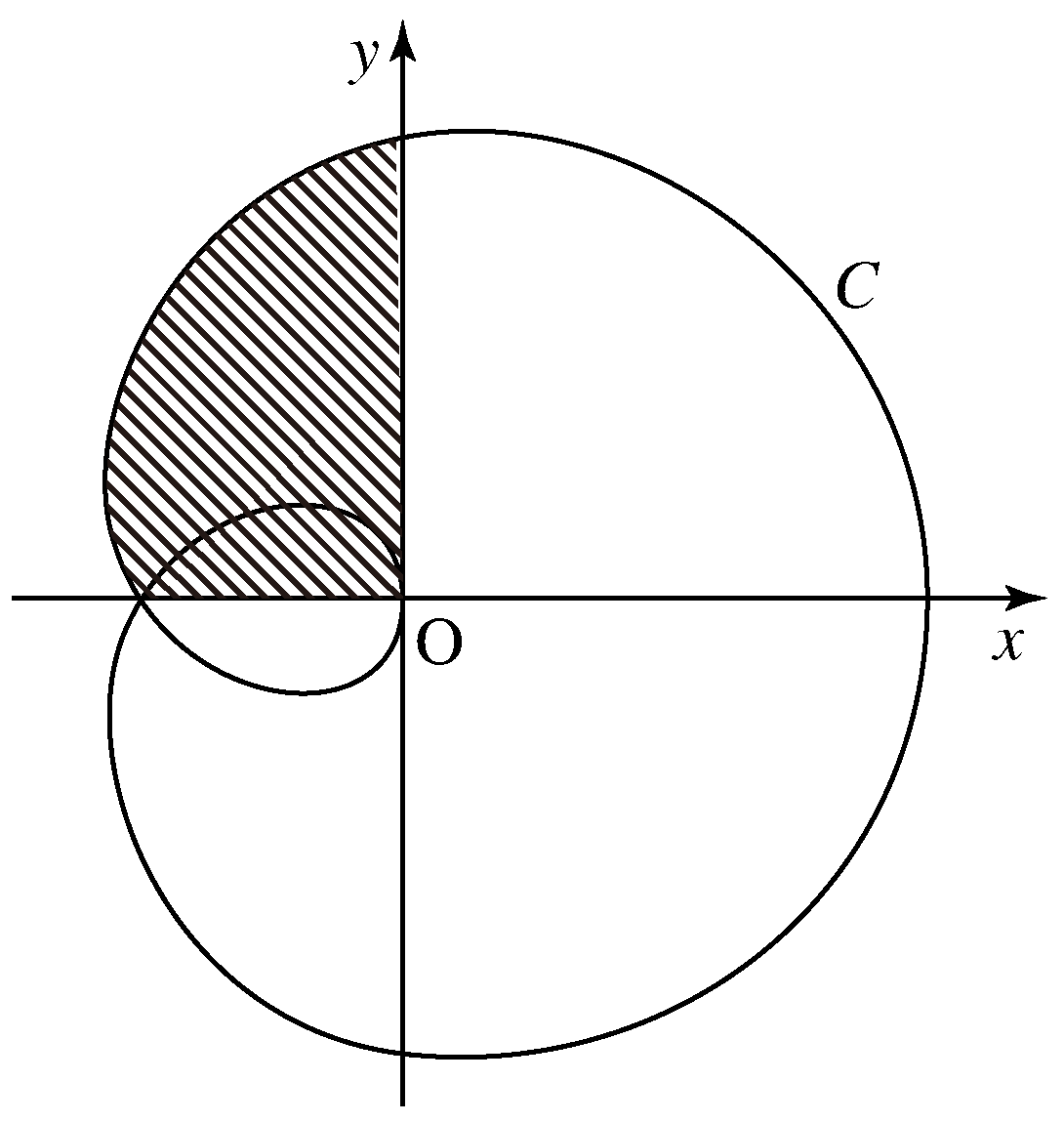 |
図1 |
図2 |
(ⅰ) 点の座標をを用いて表せ.
(ⅱ) 点を通り軸と平行な直線をとする.直線と線分のなす角を,を用いて表せ.また,の座標をを用いて表せ.
(ⅲ) 曲線と軸の共有点の座標をすべて求めよ.
(ⅳ) 曲線と軸の共有点の座標をすべて求めよ.
(ⅴ) 点の座標が最小となるときの点の座標をすべて求めよ.
(ⅵ) 曲線と軸,軸に囲まれた図2の斜線部分の面積を求めよ.