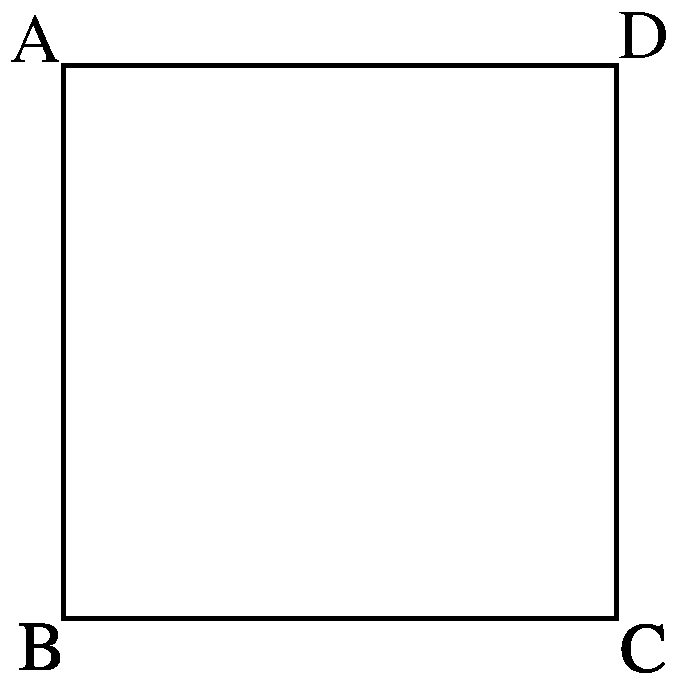
【4】 君と君がグラウンドにいる.そのグラウンドには右図のような正方形が描かれている.君の手元にはからまでの数字がつずつ描かれた枚のカードの入っている箱がある.
ここで次のような試行を考える.
君は,この箱の中から無作為にカードを枚取り出し,君にカードに描かれた数字を伝える.君はその数字にしたがって以下の規則で行動する.その後,君は,取り出したカードをもとの箱に戻す.
<規則>
・数字がのとき,移動しない.
・数字がのとき,時計回りに隣の頂点に移動する.(例 )
・数字がのとき,反時計回りに隣の頂点に移動する.(例 )
・数字がのとき,時計回りに辺に沿って対角線上の頂点に移動する.(例 )
・数字がのとき,反時計回りに辺に沿って対角線上の頂点に移動する.(例 )
最初君は頂点にいる.この試行を回繰り返した後,君が頂点にいる確率をとする.
このとき,次の問いに答えよ.
(1) である.
(2) この試行を回行った後,君が頂点にいる確率はであり,頂点にいる確率はである.したがって,である.
(3) のとき,をを用いて表すと,関係式が成り立つ.
したがって,である.