2002　九州大学　前期MathJax

【１】　次の問いに答えよ．

(1)　原点を中心とする半径$r\text{（}r>0\text{）}$の円$x^2+y^2=r^2$上の点$(a,b)$における接線の方程式は

$ax+by=r^2$

で与えられることを示せ．

(2)　円$x^2+y^2=1$と放物線$C:y=x^2+1$の両方に接する直線は$3$本ある．これら接線の方程式を求めよ．

(3)　問(2)における$3$本の接線のうち，$x$軸の正の部分と交わる接線を$l_1\text{，}x$軸に平行な接線を$l_2$とする．接線$l_1\text{，}{l}_2$および放物線$C$とで囲まれる部分の面積を求めよ．

【２】　正の整数$a$に対し，$a$の正の約数全体の和を$f(a)$で表す．ただし，$1$および$a$自身も約数とする．たとえば$f(1)=1$であり，$a=15$ならば$15$の正の約数は$1\text{，}3\text{，}5\text{，}15$なので，$f(15)=24$となる．次の問いに答えよ．

(1)　$a$が正の奇数$b$と正の整数$m$を用いて$a=2^{m}b$と表されるとする．このとき

$f(a)=(2^{m+1}-1)f(b)$

が成り立つことを示せ．必要ならば，$1+r+\cdots +r^m={\displaystyle \frac{r^{m+1}-1}{r-1}}\text{（}r\ne 1\text{）}$を用いてよい．

(2)　$a$が$2$以上の整数$p$と正の整数$q$を用いて$a=pq$と表されるとする．このとき

$f(a)\geqq (p+1)q$

が成り立つことを示せ．また，等号が成り立つのは，$q=1$かつ$p$が素数であるときに限ることを示せ．

(3)　$a=2^{2}r\text{，}b=2^{4}s$（$r\text{，}s$は正の奇数）の形をした偶数$a\text{，}b$を考える．

$\{\begin{array}{l}f(a)=2b\\ f(b)=2a\end{array}$

をみたす$a\text{，}b$を求めよ．

【３】　$▵\mathrm{AOB}$は$\mathrm{OA}=\mathrm{PB}=1$なる二等辺三角形とする．$\alpha =\angle \mathrm{AOB}$とし，線分$\mathrm{OB}$に関して$\mathrm{A}$と対称な点を${\mathrm{A}}^{\prime }$とする．次の問いに答えよ．

(1)　$\alpha <90°$とする．右図のように線分$\mathrm{OA}$上に点$\mathrm{C}$をとる．点$\mathrm{C}$を固定し，線分$\mathrm{OB}$上に点$\mathrm{D}$を折れ線$\mathrm{ADC}$の長さが最小となるようにとる．線分$\mathrm{O}{\mathrm{A}}^{\prime }$上に$\mathrm{O}{\mathrm{C}}^{\prime }=\mathrm{OC}$をみたす点${\mathrm{C}}^{\prime }$をとれば，線分$\mathrm{A}{\mathrm{C}}^{\prime }$は点$\mathrm{D}$を通ることを示せ．

(2)　$\alpha <45°$とする．線分$\mathrm{OA}$上に点$\mathrm{E}$を，線分$\mathrm{OB}$上に点$\mathrm{F}$を折れ線$\mathrm{AFE}$の長さが最小となるようにとる．このとき$\angle \mathrm{AEF}$は直角となることを示せ．

(3)　$\alpha <60°$とする．線分$\mathrm{OA}$上に点$\mathrm{G}$を，線分$\mathrm{OB}$上に点$\mathrm{H}$を折れ線$\mathrm{AHGB}$の長さが最小となるようにとる．このとき，折れ線$\mathrm{AHGB}$の長さを$\alpha$を用いて表せ．

【４】　次の問いに答えよ．

(1)　$n$を正の整数とする．どんな角度$\theta$に対しても

$\cos n\theta =2\cos \theta \cos (n-1)\theta -\cos (n-2)\theta$

が成り立つことを示せ．また，ある$n$次式$p_n(x)$を用いて$\cos n\theta$は

$\cos n\theta =p_n(\cos \theta )$

と表されることを示せ．

(2)　$p_n(x)$は$n$が偶数ならば偶関数，奇数ならば奇関数になることを示せ．

(3)　整式$p_n(x)$の定数項を求めよ．また，$p_n(x)$の$1$次の項の係数を求めよ．

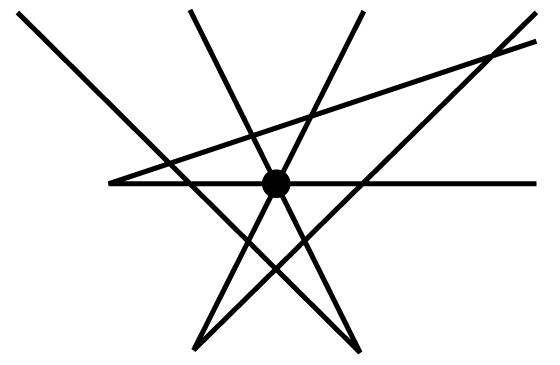
【５】　$n$を正の整数とする．平面を$n$本の直線，または$1$回折れ線でいくつかの領域に分けることを考える．ここで直線は両側に無限にのびているものとし，$1$回折れ線とは，右図のように直線の途中を$1$回折り曲げたものである．次の問いに答えよ．

(1)　平面が次の条件(ⅰ)，(ⅱ)をみたす異なる$n$本の直線のみで分割されているとする．

(ⅰ)　$n$が$2$以上ならば，どの$2$本の直線も交わる．

(ⅱ)>　$n$が$3$以上ならば，どの$3$本の直線も同一点では交わらない．

分割される平面の領域を$L_n$で表す．$n\geqq 2$のとき，$L_n$と$L_{n-1}$の間の関係式を求めよ．また，$L_n\text{（}n\geqq 1\text{）}$を求めよ．

(2)　平面が次の条件(ⅰ)，(ⅱ)をみたす異なる$n$本の$1$回折れ線のみで分割されているとする．

(ⅰ)　$n$が$2$以上ならば，どの$2$本の$1$回折れ線も異なる$4$点で交わる．

(ⅱ)　$n$が$3$以上ならば，どの$3$本の$1$回折れ線も同一点では交わらない（右図を参照せよ）．

分割される平面の領域の個数を$H_n$で表す．$H_3$を求めよ．

(3)　$H_n\text{（}n\geqq 1\text{）}$を求めよ．

【６】　空間内の図形について次の問いに答えよ．

(1)　$▵\mathrm{ABC}$の面積は

${\displaystyle \frac{1}{2}}\sqrt{{|\overrightarrow{\mathrm{AB}}|}^2{|\overrightarrow{\mathrm{AC}}|}^2-{(\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}})}^2}$

に等しいことを示せ．ここで，$\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}$はベクトル$\overrightarrow{\mathrm{AB}}$とベクトル$\overrightarrow{\mathrm{AC}}$との内積を表す．必要ならば，二つのベクトルのなす角のコサインと内積の関係式を用いてよい．

(2)　$a$を正の定数とし，右図の平行六面体$\mathrm{ABCD}‐\mathrm{EFGH}$を考える．$\left|\overrightarrow{\mathrm{AB}}\right|=\left|\overrightarrow{\mathrm{AD}}\right|=1\text{，}$$\left|\overrightarrow{\mathrm{AE}}\right|=2a$とし，$\angle \mathrm{FBC}=\angle \mathrm{BCD}=90°\text{，}\angle \mathrm{EAB}=120°$とする．面$\mathrm{EFGH}$上に点$\mathrm{P}$をとり，点$\mathrm{P}$から辺$\mathrm{EF}$上に垂線$\mathrm{PI}$を下し，点$\mathrm{P}$から辺$\mathrm{EH}$上に垂線$\mathrm{PJ}$を下ろす．$x=|\overrightarrow{\mathrm{EI}}|\text{，}$$y=|\overrightarrow{\mathrm{EJ}}|$とするとき，$▵\mathrm{ACP}$の面積を$a\text{，}x\text{，}y$を用いて表せ．

(3)　問(2)で点$\mathrm{P}$が面$\mathrm{EFGH}$上を動くとき，$▵\mathrm{ACP}$の面積の最小値を求めよ．

【７】　次の問いに答えよ．

(1)　複素数$\alpha \text{，}\beta \text{，}\gamma \text{，}\delta$は$\alpha \ne \beta \text{，}\gamma \ne \delta$をみたすとする．複素数平面上の$2$点$\alpha \text{，}\beta$を通る直線が，$2$点$\gamma \text{，}\delta$を通る直線と直交するための必要十分条件は，複素数${\displaystyle \frac{\alpha -\beta }{\gamma -\delta }}$が純虚数であることを示せ．

(2)　複素数平面上の原点を中心とする半径$1$の円$C$上に相異なる$3$点$z_1\text{，}{z}_2\text{，}{z}_3$をとり，$w_1=z_1+z_2+z_3$とおく．点$w_1$は$3$点$z_1\text{，}{z}_2\text{，}{z}_3$を頂点とする三角形の垂心になることを示せ．ここで三角形の垂心とは，各頂点から対辺またはその延長線に下ろした$3$本の垂線の交点のことであり，これら$3$本の垂線は$1$点で交わることが知られている．

(3)　問(2)において$w_2=-\overline{z_1}{z}_2{z}_3$とおく．$w_2\ne z_1$のとき，$2$点$z_2\text{，}{z}_3$を通る直線上に点$z_1$から下ろした垂線またはその延長線が円$C$と交わる点は$w_2$であることを示せ．ここで$\overline{z_1}$は$z_1$に共役な複素数である．

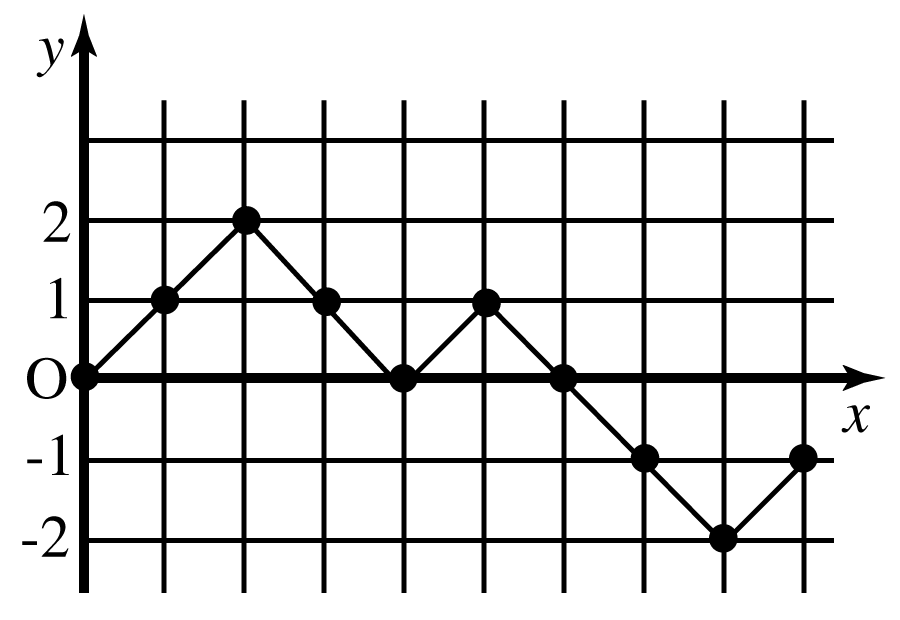
【８】　平面上の点の$x$座標と$y$座標がどちらも整数であるとき，その点を格子点という．与えられた格子点を第$1$番目とし，この点から右斜め$45°\text{，}$または右斜め$-45°$の方向にもっとも近い第$2$番目の格子点をとり，この$2$点を線分で結ぶ．同様にして第$2$番目の格子点から第$3$番目の格子点をとり，第$2$番目と第$3$番目を線分で結ぶ．以下これを有限回繰り返し，こうしてできる線分をつないだものを折れ線グラフということにする．右図に原点$\mathrm{O}$と格子点$(9,-1)$を結ぶ折れ線グラフの例を示す．次の問いに答えよ．

(1)　$n$は正の整数，$k$は$0\leqq k\leqq n$なる整数とする．原点$\mathrm{O}$と格子点$(n,k)$を結ぶ折れ線グラフが存在するための必要十分条件は$n+k$が偶数であることを示せ．また，この必要十分条件がみたされているとき，原点$\mathrm{O}$と格子点$(n,k)$を結ぶ折れ線グラフの数を求めよ．

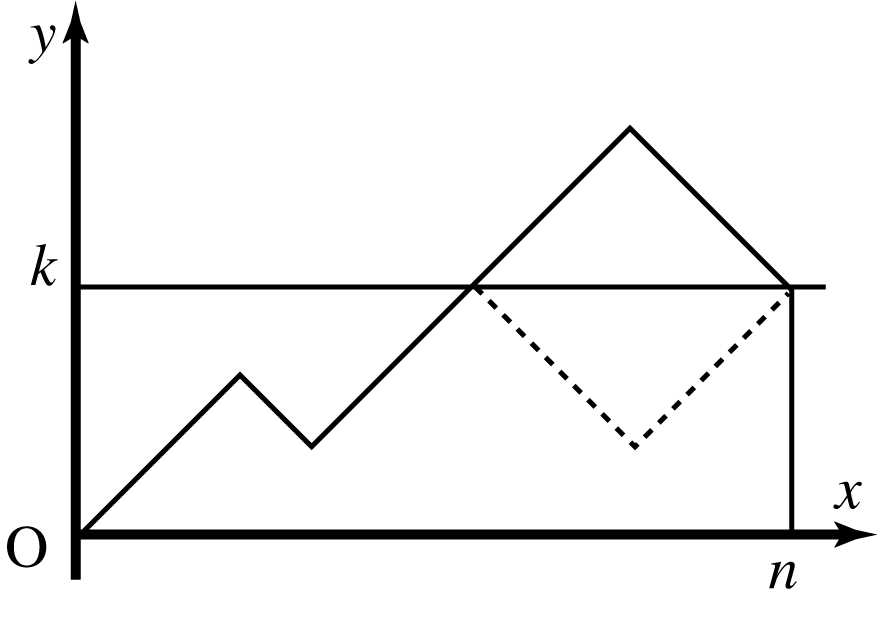
(2)　$n$は$2$以上の整数，$k$は$0\leqq k\leqq n-2$なる整数で，$n+k$は偶数とする．原点$\mathrm{O}$と格子点$(n,k)$を結ぶ折れ線グラフであって格子点$(0,k)\text{，}(1,k)\text{，}\cdots \text{，}(n-2,k)$の少なくとも$1$つを通る折れ線グラフの数は，原点$\mathrm{O}$と格子点$(n-k,k+1)$を結ぶ折れ線グラフの数の$2$倍に等しいことを示せ（必要ならば右図を参考にせよ）．

(3)　コインを$9$回投げる．$1$回から$i$回までの試行において，表の出た回数から裏の出た回数を引いた数を$T_i$で表す．このとき各格子点$(i,T_i)\text{，}i=0\text{，}1\text{，}2\text{，}\cdots \text{，}9\text{，}$を順番に線分でつなげば折れ線グラフが得られる．ただし，$T_0=0$とする．$T_9=3$が起きたとき，どの$T_i\text{（}i=1\text{，}2\text{，}\cdots \text{，}7\text{）}$も$3$にならない条件つき確率を求めよ．

【１】　平面上を運動する点$\mathrm{P}(x,y)$の時刻$t$での$x$座標と$y$座標が

$\{\begin{array}{l}x={\displaystyle \frac{e^t-e^{-t}}{2}}\\ y={\displaystyle \frac{e^t+e^{-t}}{2}}\end{array}$

で表されている．ただし，$e$は自然対数の底である．原点を$\mathrm{O}\text{，}$点$(0,1)$を$\mathrm{M}$とする．$t$が$t\geqq 0$の範囲で変化したとき点$\mathrm{P}$が描く曲線を$C$とする．時刻$t$において，曲線$C\text{，}$線分$\mathrm{OM}\text{，}$および線分$\mathrm{OP}$で囲まれる図形の面積を$A(t)$で表し，曲線$C$と線分$\mathrm{MP}$で囲まれる図形の面積を$S(t)$で表す．次の問いに答えよ．

(1)　点$\mathrm{P}(x,y)$の座標$x\text{，}y$に対して$y$を$x$を用いて表せ．

(2)　時刻$t$を用いて$A(t)$と$S(t)$を表せ．

(3)　$A(t)-S(t)$が最大となる時刻$t$を求めよ．

【２】　正の整数$a$に対し，$a$の正の約数全体の和を$f(a)$で表す．ただし，$1$および$a$自身も約数とする．たとえば$f(1)=1$であり，$a=15$ならば$15$の正の約数は$1\text{，}3\text{，}5\text{，}15$なので，$f(15)=24$となる．次の問いに答えよ．

(1)　$a$が正の奇数$b$と正の整数$m$を用いて$a=2^{m}b$と表されるとする．このとき

$f(a)=(2^{m+1}-1)f(b)$

が成り立つことを示せ．

(2)　$a$が$2$以上の整数$p$と正の整数$q$を用いて$a=pq$と表されるとする．このとき

$f(a)\geqq (p+1)q$

が成り立つことを示せ．また，等号が成り立つのは，$q=1$かつ$p$が素数であるときに限ることを示せ．

(3)　正の偶数$a\text{，}b$は，ある整数$m\text{，}n$とある奇数$r\text{，}s$を用いて$a=2^{m}r\text{，}b=2^{n}s$のように表すことができる．このとき$a\text{，}b$が

$\{\begin{array}{l}f(a)=2b\\ f(b)=2a\end{array}$

をみたせば，$r\text{，}s$は素数であり，かつ$r=2^{n+1}-1\text{，}s=2^{m+1}-1$となることを示せ．

【３】　次の問いに答えよ．

(1)　すべての正の実数$x\text{，}y$に対して，不等式

$x\log x-x\log y-x+y\geqq 0$

が成り立つことを示せ．ここで$\log$は自然対数を表す．

(2)　$a\text{，}b$は実数で$a<b$とする．関数$f(x)$と$g(x)$は閉区間$[a,b]$で正の値をとる連続関数で

${\displaystyle {\int }_a^b}f(x)dx={\displaystyle {\int }_a^b}g(x)dx$

をみたす．このとき，不等式

${\displaystyle {\int }_a^b}f(x)\log \log f(x)dx\geqq {\displaystyle {\int }_a^b}f(x)\log g(x)dx$

が成り立つことを示せ．

(3)　$a\text{，}b$は実数で$a<b$とする．閉区間$[a,b]$で正の値をとる連続関数$f(x)$に対し正の実数$M$を

$M={\displaystyle \frac{1}{b-a}}{\displaystyle {\int }_a^b}f(x)dx$

とする．不等式

${\displaystyle \frac{1}{b-a}}{\displaystyle {\int }_a^b}f(x)\log f(x)dx\geqq M\log M$

が成り立つことを示せ．

【４】　空間内の図形について次の問いに答えよ．

(1)　$▵\mathrm{ABC}$の面積は

${\displaystyle \frac{1}{2}}\sqrt{{|\overrightarrow{\mathrm{AB}}|}^2{|\overrightarrow{\mathrm{AC}}|}^2-{(\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}})}^2}$

に等しいことを示せ．ここで，$\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}$はベクトル$\overrightarrow{\mathrm{AB}}$とベクトル$\overrightarrow{\mathrm{AC}}$との内積を表す．必要ならば，二つのベクトルのなす角のコサインと内積の関係式を用いてよい．

(2)　右図の平行六面体$\mathrm{ABCD}‐\mathrm{EFGH}$を考える．$\left|\overrightarrow{\mathrm{AB}}\right|=\left|\overrightarrow{\mathrm{AD}}\right|=1\text{，}$$\left|\overrightarrow{\mathrm{AE}}\right|=2$とし，$\angle \mathrm{FBC}=\angle \mathrm{BCD}={\displaystyle \frac{\pi }{2}}\text{，}$$\angle \mathrm{EAB}=\theta$とする．ここで$\theta$は$0<\theta <\pi$なる定数とする．面$\mathrm{EFGH}$上に点$\mathrm{P}$をとり，点$\mathrm{P}$から辺$\mathrm{EF}$上に垂線$\mathrm{PI}$を下し，点$\mathrm{P}$から辺$\mathrm{EH}$上に垂線$\mathrm{PJ}$を下ろす．$x=\left|\overrightarrow{\mathrm{EI}}\right|\text{，}$$y=\left|\overrightarrow{\mathrm{EJ}}\right|$とするとき，$▵\mathrm{ACP}$の面積を$\theta \text{，}x\text{，}y$を用いて表せ．

(3)　問(2)で点$\mathrm{P}$が面$\mathrm{EFGH}$上を動くとき，$▵\mathrm{ACP}$の面積の最小値を求めよ．

【５】　複素数平面上の原点を中心とする半径$1$の円$C$上に相異なる$3$点$z_1\text{，}{z}_2\text{，}{z}_3$をとる．次の問いに答えよ．

(1)　$w_1=z_1+z_2+z_3$とおく．点$w_1$は$3$点$z_1\text{，}{z}_2\text{，}{z}_3$を頂点とする三角形の垂心になることを示せ．ここで三角形の垂心とは，各頂点から対辺またはその延長線上に下ろした$3$本の垂線の交点のことであり，これら$3$本の垂線は$1$点で交わることが知られている．

(2)　$w_2=-\overline{z_1}{z}_2{z}_3$とおく．$w_2\ne z_1$のとき，$2$点$z_2\text{，}{z}_3$を通る直線上に点$z_1$から下ろした垂線またはその延長線が円$C$と交わる点は$w_2$であることを示せ．ここで$\overline{z_1}$は$z_1$に共役な複素数である．

(3)　$2$点$z_2\text{，}{z}_3$を通る直線とこの直線上に点$z_1$から下ろした垂線との交点は，点$w_1$と点$w_2$を結ぶ線分の中点であることを示せ．ただし，$w_1=w_2$のときは，$w_1$と$w_2$の中点は$w_1$と解釈する．

【６】　平面上の点の$x$座標と$y$座標がどちらも整数であるとき，その点を格子点という．与えられた格子点を第$1$番目とし，この点から右斜め$45°\text{，}$または右斜め$-45°$の方向にもっとも近い第$2$番目の格子点をとり，この$2$点を線分で結ぶ．同様にして第$2$番目の格子点から第$3$番目の格子点をとり，第$2$番目と第$3$番目を線分で結ぶ．以下これを有限回繰り返し，こうしてできる線分をつないだものを折れ線グラフということにする．右図に原点$\mathrm{O}$と格子点$(9,-1)$を結ぶ折れ線グラフの例を示す．次の問いに答えよ．

(1)　$n$は正の整数，$k$は$0\leqq k\leqq n$なる整数とする．原点$\mathrm{O}$と格子点$(n,k)$を結ぶ折れ線グラフが存在するための必要十分条件は$n+k$が偶数であることを示せ．また，この必要十分条件がみたされているとき，原点$\mathrm{O}$と格子点$(n,k)$を結ぶ折れ線グラフの数を求めよ．

(2)　$n$は$2$以上の整数，$k$は$0\leqq k\leqq n-2$なる整数で，$n+k$は偶数とする．原点$\mathrm{O}$と格子点$(n,k)$を結ぶ折れ線グラフであって格子点$(0,k)\text{，}(1,k)\text{，}\cdots \text{，}(n-2,k)$の少なくとも$1$つを通る折れ線グラフの数は，原点$\mathrm{O}$と格子点$(n-1,k+1)$を結ぶ折れ線グラフの数の$2$倍に等しいことを示せ．

(3)　コインを$9$回投げる．$1$回から$i$回までの試行において，表の出た回数から裏の出た回数を引いた数を$T_i$で表す．このとき各格子点$(i,T_i)\text{，}i=0\text{，}1\text{，}2\text{，}\cdots \text{，}9\text{，}$を順番に線分でつなげば折れ線グラフが得られる．ただし，$T_0=0$とする．$T_9=3$が起きたとき，どの$T_i\text{（}i=1\text{，}2\text{，}\cdots \text{，}7\text{）}$も$3$にならない条件つき確率を求めよ．

【７】　平面上の点$\mathrm{P}$の$x$座標と$y$座標が，変数$\theta$の関数$f(\theta )={\displaystyle \frac{{(\theta -\pi )}^2}{2{\pi }^2}}+{\displaystyle \frac{1}{2}}$を用いて

$\{\begin{array}{l}x=f(\theta )\cos \theta \\ y=f(\theta )\sin \theta \end{array}$

と表されている．$\theta$が$0\leqq \theta \leqq 2\pi$の範囲で変化したとき，点$\mathrm{P}$が描く曲線を$C$とする．点$\mathrm{P}$を$\mathrm{P}(\theta )$で表し，${\mathrm{P}}_1=\mathrm{P}(0)\text{，}{\mathrm{P}}_2=\mathrm{P}\left({\displaystyle \frac{\pi }{2}}\right)\text{，}{\mathrm{P}}_3=\mathrm{P}(\pi )$とおく．次の問いに答えよ．

(1)　方程式

${\displaystyle \frac{{(x-\alpha )}^2}{a^2}}+{\displaystyle \frac{{(y-\beta )}^2}{b^2}}=1\text{（}a>0\text{，}b>0\text{）}$

で与えられる楕円が点${\mathrm{P}}_1$を通るとする．このとき，点${\mathrm{P}}_3$がこの楕円の内部に含まれる（ただし，楕円の上にない）ための必要十分条件を$\alpha$のみを用いて表せ．

(2)　点${\mathrm{P}}_2$における曲線$C$の接線を$l$とする．$l$の方程式を求めよ．

(3)　次の条件(ⅰ)，(ⅱ)，(ⅲ)をみたす楕円$D$を考える．

(ⅰ)　$D$の軸の一つは$x$軸上にある．

(ⅱ)　$D$は点${\mathrm{P}}_1\text{，}{\mathrm{P}}_2$を通る．

(ⅲ)　点${\mathrm{P}}_2$における$D$の接線は$l$である．

　このとき，点${\mathrm{P}}_3$は楕円$D$の内部に含まれるかどうか判定せよ．

【８】　正の実数$a$の$3$乗根$\sqrt[3]{a}$を近似することを考える．与えられた$2$以上の整数$p$に対して関数$f(x)\text{，}g(x)$を

$\{\begin{array}{l}f(x)=x^p-a{x}^{p-3}\\ g(x)=x-{\displaystyle \frac{f(x)}{f^{\prime }(x)}}\end{array}$

とする．ここで$f^{\prime }(x)$は$f(x)$の導関数である．次の問いに答えよ．

(1)　$g(x)-\sqrt[3]{a}$は

$g(x)-\sqrt[3]{a}={(x-\sqrt[3]{a})}^2\times {\displaystyle \frac{x\text{の}2\text{次式}}{x\text{の}3\text{次式}}}$

の形で表されることを示せ．

(2)　$p=2$とする．このとき，$g(x)-\sqrt[3]{a}$は

$g(x)-\sqrt[3]{a}={(x-\sqrt[3]{a})}^3\times {\displaystyle \frac{x\text{の}1\text{次式}}{x\text{の}3\text{次式}}}$

の形で表されることを示せ．

(3)　$a=9\text{，}p=2$とする．$2<\sqrt[3]{9}<2.1$に注意して，不等式

$0<\sqrt[3]{9}-g(2)<{\displaystyle \frac{1}{1000}}$

が成り立つことを示せ．また，$\sqrt[3]{9}$を小数第$3$位まで求めよ（すなわち，小数第$4$位以下を切り捨てよ）．

【９】　$2$次の正方行列$A$が零行列でなく$A^2=A$をみたすとき，べき等行列という．次の問いに答えよ．

(1)　行列$A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$はべき等行列であり，かつ$ad-bc\ne 0$とする．このとき，$A$を求めよ．

(2)　行列$A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$は$ad-bc=0$をみたすとする．このとき，$A$がべき等行列であるための必要十分条件を$a$と$d$のみを用いて表せ．

(3)　行列$A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\text{，}B=\left(\begin{array}{cc}e& f\\ g& h\end{array}\right)$はともにべき等行列とする．$A+B$がべき等行列になるとき，$A+B$を求めよ．また，そのような$A\text{，}B$の組を一つあげよ．