2006　慶応義塾大学　環境情報学部MathJax

【１】

(1)　多項式$f(x)$で定義される曲線$y=f(x)$が直線$y=g(x)$に点$(s,t)$で接するとは，$f(x)-g(x)$が${(x-s)}^2$で割り切れることであり，このとき$y=g(x)$は$y=f(x)$の$(s,t)$における接線である．

　いま曲線$f(x)=x^2(x^2-2x-3)$が直線$g(x)=ax+b$と異なる$2$点$\mathrm{P}=(p_1,p_2)\text{，}\mathrm{Q}=(q_1,q_2)\text{，}{p}_1<q_1\text{，}$で接している．このとき

$a=\boxed{\text{(1)}}\boxed{\text{(2)}}\text{，}b=\boxed{\text{(3)}}\boxed{\text{(4)}}\text{，}{p}_1=\boxed{\text{(5)}}\boxed{\text{(6)}}\text{，}{q}_1=\boxed{\text{(7)}}\boxed{\text{(8)}}$

である．

【１】

(2)　すべての実数$x$に対して

$x^2(x^2-2x-3)-ax-b\geqq 0$

が成り立つような$(a,b)$全体の集合は，実数$p$を用いて次のように表される．

• i)　$p\leqq \boxed{\text{(9)}}\boxed{\text{(10)}}$のとき，$a=4p^3-6p^2-6p\text{，}b\leqq \boxed{\text{(11)}}\boxed{\text{(12)}}{p}^4+\boxed{\text{(13)}}{p}^3+\boxed{\text{(14)}}{p}^2$
• ii)　$\boxed{\text{(9)}}\boxed{\text{(10)}}<p\leqq \boxed{\text{(15)}}\boxed{\text{(16)}}$のとき，$a=-4\text{，}b\leqq \boxed{\text{(17)}}\boxed{\text{(18)}}$
• iii)　$p>\boxed{\text{(15)}}\boxed{\text{(16)}}$のとき，$a=4p^3-6p^2-6p\text{，}b\leqq \boxed{\text{(11)}}\boxed{\text{(12)}}{p}^4+\boxed{\text{(13)}}{p}^3+\boxed{\text{(14)}}{p}^2$

【２】　$\mathrm{O}$を中心とする半径$1$の円に正五角形$\mathrm{ABCDE}$が内接している．

(1)　

${\displaystyle \frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\boxed{\text{(19)}}+\sqrt{\boxed{\text{(20)}}}}{\boxed{\text{(21)}}}}$

(2)　$\angle \mathrm{BAD}=\theta$としたとき

$\cos \theta ={\displaystyle \frac{\boxed{\text{(22)}}\boxed{\text{(23)}}+\sqrt{\boxed{\text{(24)}}}}{\boxed{\text{(25)}}}}$

(3)　線分$\mathrm{OA}$の中点を$\mathrm{M}$としたとき，線分$\mathrm{AM}\text{，}\mathrm{BM}\text{，}\mathrm{CM}\text{，}\mathrm{DM}\text{，}\mathrm{EM}$の長さの積は

${\displaystyle \frac{\boxed{\text{(26)}}\boxed{\text{(27)}}}{\boxed{\text{(28)}}\boxed{\text{(29)}}}}$

である．

【３-1】　選択肢から最も適切なものを選びその番号を解答欄に記入しなさい．

　自然数$n$を含む命題$\mathrm{P}(n)$がすべての自然数$n$に対して成り立つことを証明するには，数学的帰納法の変形として，つぎの$3$つを示せばよい．

• (A)　$\mathrm{P}(1)\text{，}\mathrm{P}(2)$が成り立つ．
• (B)　$\mathrm{P}(k)\text{，}k\geqq 2\text{，}$が成り立つとき，$\mathrm{P}(2k)$も成り立つ．
• (C)　$\mathrm{P}(k)\text{，}k\geqq 2\text{，}$が成り立つとき，$\mathrm{P}(k-1)$も成り立つ．

　この方法を用いて，つぎの命題$\mathrm{P}(n)$がすべての自然数$n$に対して成り立つことを証明する．

命題$\mathrm{P}(n):$すべての$x_1\text{，}{x}_2\text{，}\cdots \text{，}{x}_n\geqq 0$に対して

${\displaystyle \frac{x_1+x_2+\cdots +x_n}{n}}\geqq {(x_1{x}_2\cdots x_n)}^{\frac{1}{n}}$

証明$:x_i\text{（}1\leqq i\leqq n\text{）}$に$0$が含まれるときは，右辺は$0$となるので命題は明らか．よって以下の議論ではすべての$x_1\text{，}{x}_2\text{，}\cdots \text{，}{x}_n$は$\boxed{\text{(31)}}$より大きいとする．

(A)　$n=1$のとき，両辺とも$x_1$となり$\mathrm{P}(1)$は成り立つ．$n=2$のときも

$x_1-2\sqrt{x_1{x}_2}+x_2={(\sqrt{x_1}-\sqrt{x_2})}^2\geqq 0$

より$\mathrm{P}(2)$は成り立つ．

(B)　$n=k\text{，}k\geqq 2\text{，}$のとき命題は成り立つとする．

$\begin{array}{ll}{\displaystyle \frac{x_1+x_2+\cdots +x_{\boxed{\text{(32)}}}}{\boxed{\text{(33)}}}}& ={\displaystyle \frac{x_1+x_2+\cdots +x_k}{\boxed{\text{(33)}}}+\frac{x_{\boxed{\text{(34)}}}+\cdots +x_{\boxed{\text{(35)}}}}{\boxed{\text{(33)}}}}\\ & \geqq {\displaystyle \frac{{(x_1{x}_2\cdots x_k)}^{\frac{1}{\boxed{\text{(36)}}}}}{\boxed{\text{(37)}}}+\frac{{(x_{\boxed{\text{(34)}}}\cdots x_{\boxed{\text{(35)}}})}^{\frac{1}{\boxed{\text{(36)}}}}}{\boxed{\text{(37)}}}}\\ & \geqq {(x_1{x}_2\cdots x_{\boxed{\text{(38)}}})}^{\frac{1}{\boxed{\text{(39)}}}}\end{array}$

となり，$\mathrm{P}(2k)$が成り立つことが分かる．ここで最後の式の変形では$\mathrm{P}(\boxed{\text{(40)}})$を用いている．

(C)　$n=k\text{，}k\geqq 2\text{，}$のとき命題は成り立つとする．とくに

$x_k={\displaystyle \frac{x_1+x_2+\cdots +x_{k-1}}{k-1}}$

とすれば，${x_k}^{\boxed{\text{(41)}}}\geqq x_1{x}_2\cdots x_k$となる．両辺を$x_k$で割れば

${\displaystyle \frac{x_1+x_2+\cdots +x_{k-1}}{k-1}}=x_k\geqq {(x_1{x}_2\cdots x_{k-1})}^{\frac{1}{k-1}}$

となる．よって$\mathrm{P}(k-1)$が成り立つことが分かる．

　以上の(A)，(B)，(C)により命題$\mathrm{P}(n)$はすべての自然数$n$に対して成り立つ．

[選択肢]

• (0)　$0$
• (1)　$1$
• (2)　$2$
• (3)　$k-1$
• (4)　$k$
• (5)　$k+1$
• (6)　$2k$
• (7)　$n-1$
• (8)　$n$
• (9)　$n+1$

【３-2】　以下のプログラムは自然数Nを与えたとき，その約数を順次印刷するものである．選択肢から最も適切なものを選びその番号を解答欄に記入しなさい．

• 100 INPUT N
• 110 FOR $\boxed{\text{(42)}}\boxed{\text{(43)}}$ = $\boxed{\text{(44)}}\boxed{\text{(45)}}$ TO $\boxed{\text{(46)}}\boxed{\text{(47)}}$
• 120 B= $\boxed{\text{(48)}}\boxed{\text{(49)}}$ -A * $\boxed{\text{(50)}}\boxed{\text{(51)}}$ ( $\boxed{\text{(52)}}\boxed{\text{(53)}}$ / $\boxed{\text{(54)}}\boxed{\text{(55)}}$ )
• 130 IF $\boxed{\text{(56)}}\boxed{\text{(57)}}$ = 0 THEN PRINT $\boxed{\text{(58)}}\boxed{\text{(59)}}$
• 140 NEXT A
• 150 END

[選択肢]

• (01)　1
• (02)　2
• (03)　0
• (04)　-1
• (05)　A
• (06)　B
• (07)　C
• (08)　N
• (09)　R
• (10)　K
• (11)　FOR
• (12)　INPUT
• (13)　NEXT
• (14)　PRINT
• (15)　THEN
• (16)　STEP
• (17)　END
• (18)　INT
• (19)　SQR
• (20)　LET

【４】　一直線上を正の方向に運動する物体の速度を観測し，下の表のような時刻$x$における速度$v\left(x\right)$が得られた．以下の議論では観測値の測定誤差はないものとする．

　$v\left(x\right)$が$x$の二次関数で表されるとすれば

$v\left(x\right)=\boxed{\text{(60)}}\boxed{\text{(61)}}{x}^2+\boxed{\text{(62)}}\boxed{\text{(63)}}x+\boxed{\text{(64)}}\boxed{\text{(65)}}$

である．物体の移動した道のりは速度の積分であり，この運動の場合，$0\leqq x\leqq 2$において$v\left(x\right)\geqq 0$であるから，道のりは$v\left(x\right)$と$x$軸で囲まれる部分の面積となる．

　$\mathrm{A}$君は二次関数の積分ができたので，道のりを${\displaystyle \frac{\boxed{\text{(66)}}\boxed{\text{(67)}}}{\boxed{\text{(68)}}\boxed{\text{(69)}}}}$と求めることができた．

　$\mathrm{B}$君は二次関数の積分公式を知らなかった．そこで上述の面積の計算を，二次関数を折れ線で近似して計算することにした．すなわち$x_0=0.0\text{，}{x}_1=0.2\text{，}{x}_2=0.4\text{，}\cdots \text{，}{x}_{10}=2.0$としたとき，各$k=0\text{，}1\text{，}2\text{，}\cdots \text{，}9$に対して，$v(x)\text{，}x=x_k\text{，}x=x_{k+1}\text{，}x$軸で囲まれる部分の面積を，点$(x_k,0)\text{，}(x_k,v(x_k))\text{，}(x_{k+1},v(x_{k+1}))\text{，}(x_{k+1},0)\text{，}(x_k,0)$を順に線分で結んで得られる台形（$k=0\text{，}9$のときは三角形）の面積で近似することにした．このようにすると道のりの近似値として$\boxed{\text{(70)}}.\boxed{\text{(71)}}\boxed{\text{(72)}}$（小数表示）が得られた．

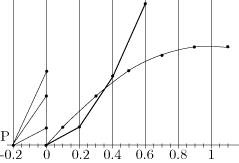
　$\mathrm{C}$君は$\mathrm{B}$君の計算を見ていて次のような方法を思いついた．右の図のように点$\mathrm{P}$を$(-0.2,0)$にとる．各$k=0\text{，}1\text{，}2\text{，}\cdots \text{，}9$に対して，$2$点$(x_k,v(x_k))\text{，}(x_{k+1},v(x_{k+1}))$を結ぶ線分の中点を$({\displaystyle \frac{x_k+x_{k+1}}{2}},y_k)$とする．ここで$\mathrm{P}$と${\mathrm{Q}}_k=(0,y_k)$をつなぎ，その線分を$\mathrm{P}{\mathrm{Q}}_k$とする．$\mathrm{P}{\mathrm{Q}}_k$を$x$軸に沿って平行移動し，区間$x_k\leqq x\leqq x_{k+1}$の中にいれる．次に$y$軸に沿って平行移動し，図のようにその左端と$\mathrm{P}{\mathrm{Q}}_{k-1}$を平行移動したものの右端とをつなぐ．ただし，$\mathrm{P}{\mathrm{Q}}_0$を移動したものの左端は原点とする．

　$k=0\text{，}1\text{，}2\text{，}\cdots \text{，}9$と順次この操作を行ってできた折れ線の右端の$y$座標は$\boxed{\text{(73)}}\boxed{\text{(74)}}.\boxed{\text{(75)}}$（小数表示）であり，これに$\boxed{\text{(76)}}.\boxed{\text{(77)}}$（小数表示）を掛ければ$\mathrm{B}$君の求めた値となる．

【５】　関数が与えられたとき，関数に対応する縞模様をスクリーンに投影する．下記の図Aは$f(x)=\cos x\text{（}-180°\leqq x\leqq 180°\text{）}$に対応する縞模様であり，投影の仕方は以下の通りである．

• (a)　スクリーンの下辺を水平方向の座標$-180°\leqq x\leqq 180°$とする．またスクリーンの左辺を垂直方向の座標軸$-\leqq y\leqq 1$とする．
• (b)　$(x,-1)$と$(x,1)$を結ぶ線分に色（白黒の濃淡）を対応させる．このとき，関数の値$f(x)$が小さいほど線分は濃くなり，大きいほど淡くなる．$f(x)$が最小値のとき黒，最大値のとき白とする．

　実際，$f(x)=\cos x\text{（}-180°\leqq x\leqq 180°\text{）}$は$x=0°$で最大値$1$をとり，$x=-180°\text{，}180°$で最小値$-1$をとるので，縞模様は$x=0°$のところが白となり，$x=-180°\text{，}180°$のところが黒となる．

　図Bのような白の帯が$3$本見える縞模様を

$g(x)=a\cos (cx)-b\sin (cx)\text{（}a\text{，}b\text{，}c\geqq 0\text{，}-180°\leqq x\leqq 180°\text{）}$

に対応させてスクリーンに投影させたい．ただし，$x=0°$のところの値は図A，Bとも同じであるが，図Bの最も濃いところの$g(x)$の値は，図Aの最も濃いところの$f(x)$の値の$\sqrt{2}$倍である．このとき

$a=\boxed{\text{(78)}}\boxed{\text{(79)}}\text{，}b=\boxed{\text{(80)}}\boxed{\text{(81)}}\text{，}c=\boxed{\text{(82)}}\boxed{\text{(83)}}$

である．